Solving a Sourcing Problem With Spreadsheets
In this blog:
we highlight the conveniences and limitations of using spreadsheets to make a sourcing decision;
show how the lack of a systematic approach can miss opportunities to save up to 17% on total costs;
illustrate the effectiveness of a simple greedy approach;
emphasize the benefit of knowing the best possible solution, in this case, obtained with mathematical optimization; and
we provide the spreadsheet we created so anyone can play the decision-making game.
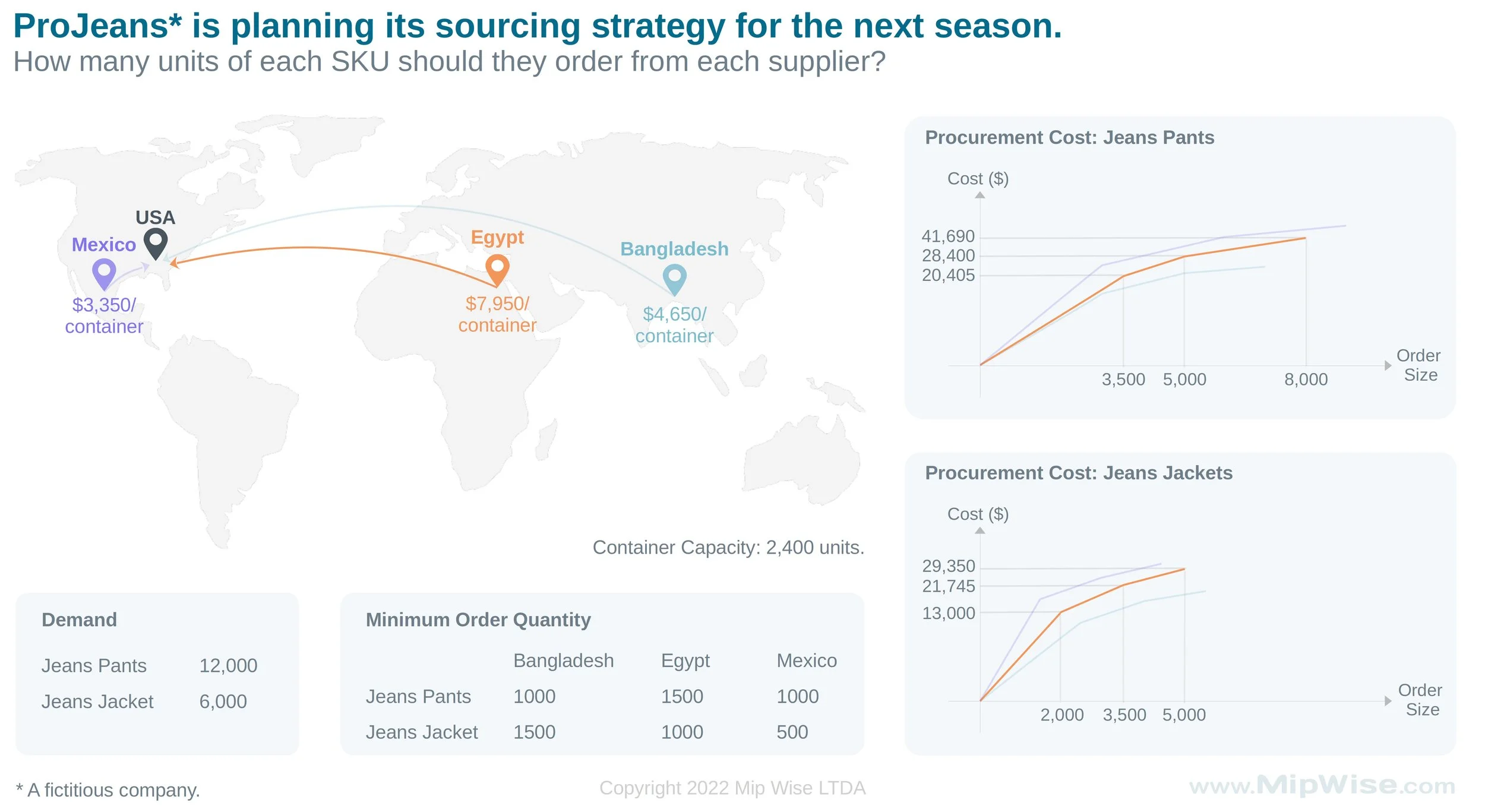
If you were a business analyst or business planner tasked with making the sourcing decision depicted in this chart, how would you go about doing so?
Specifically, how many pants and jackets do you buy from each supplier, given that each has a price function and you need to meet the demand for each SKU while minimizing procurement and shipping costs?
Visit the ProJeans use case for a detailed statement of the business problem.
The motivation
From what we've heard, even when business owners have access to decision-making resources (like off-the-shelf software or a modeling platform like Supply Chain Guru), many of them have a strong tendency to go back to spreadsheets. Instead of wondering why this happens, we got curious about the following question:
Is there any problem with using spreadsheets to support a business decision like the one in this use case?
As decision scientists, we don’t use spreadsheets very often. When we think about making decisions from data, we think of databases, Pandas data frames, modeling, and algorithms. But to answer this question, we committed to put ourselves in the shoes of a business practitioner and try to solve the ProJeans use case using only a spreadsheet.
The main takeaway
What we found was that for the current version of the problem, a spreadsheet approach can be quite effective. However, depending on the data and how we look for good solutions, we can easily miss out on the opportunity to save up to 17% on total procurement and shipping costs.
The thought process
First, we solved the problem using mathematical optimization in Python. This is how we know for sure the cost of the best possible solution, which we use to assess the quality of any solution we derive using the spreadsheet.
We then created the spreadsheet. It has several worksheets that contain all the input data and it has a worksheet dedicated to calculations, where we enter formulas to compute costs and highlight violated business requirements. Based on what we've seen, this should be close to what business people do (leave a comment if you would do differently).
When the spreadsheet was ready, we first tried to get the order quantities in a very naive way. Not surprisingly, the results weren't good. The optimal cost was 17% below the total costs of the solutions we found.
We then derived two solutions more systematically using a greedy approach, first aiming to minimize the acquisition cost and then the shipping cost. The result this time was much better, only 8.63% (or 13.12% if the greedy algorithm is a bit naive) and 7.70% far from the optimal solution.
We challenge you to play with our spreadsheet and find a solution that saves more on the total cost.
While 7.70% might seem like a small difference, it's important to keep in mind that this was not a scientific experiment and the outcomes can vary significantly. In fact, we tested instances where the greedy approach provided almost the optimal solution, but also instances where it performed surprisingly poorly.
To keep in mind
Increasing the number of SKUs and suppliers, or accounting for realistic complexities such as multiple container sizes, container capacity based on the volume or weight of each SKU, and incremental order quantities, can make it much harder to find good solutions using an ad-hoc approach.
In all cases, how can a decision maker using only a spreadsheet know that there isn't a solution that reduces the cost by another 10%?
To find a proven optimal solution, we need a more scientific approach like the one we implemented using mathematical optimization (for which spreadsheets are not well suited).